References - My Code School

Binary Tree

Binary tree is a special tree where a tree can have at most 2 children.

This means that a tree can have 0, 1 or 2 children, and still it can be a valid binary tree. So, based on this definition, all of these are valid binary trees.

For a binary tree, maximum number of nodes at level 'n' is 2^n.

Types of Binary Trees:

• Strict / Proper / Full Binary Tree
• Complete Binary Tree
• Perfect Binary Tree
• Balanced Binary Tree

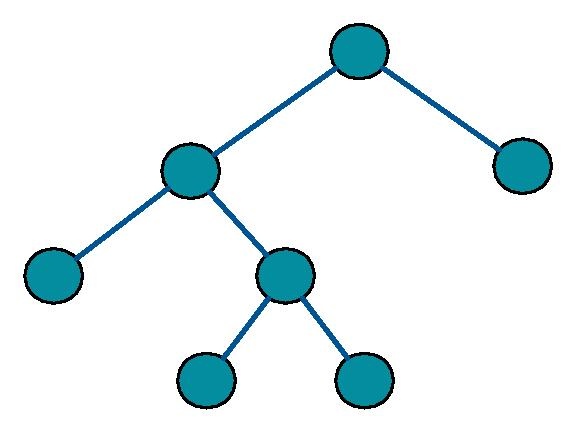
Strict / Proper / Full Binary Tree

Strict or Proper Binary Tree is defined as a tree where each node can have either 0 or 2 children.

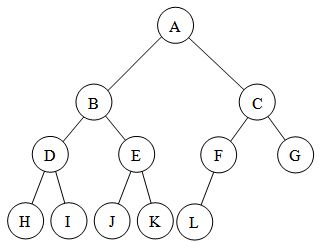
Complete Binary Tree

A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible. The tree shown below is a complete binary tree as all the nodes are as far left as possible.

A complete binary tree always contains between 1 and 2^(n-1) nodes at the last level 'n'.

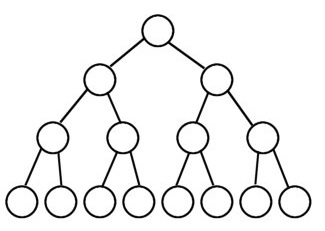
Perfect Binary Tree

A perfect binary tree is a binary tree in which all nodes have two children and all leaves have the same depth or same level.

Technically, a perfect binary tree is always a complete binary tree and a full / strict / proper binary tree.

Properties of Perfect Binary Tree

Since there can be maximum 2 child nodes for any given node, there can be maximum 2^n number of nodes at 'n' level.

So, for a tree with height 'h', number of nodes = 2^0 + 2^1 + 2^2 + ..... + 2^h = [2^(h+1)] -1.

• Maximum number of nodes in a binary tree with height 'h' = [ 2 ^ (h+1) ] - 1
• Height of a perfect binary tree with 'n' nodes = [ log with base 2 of (n + 1) ] - 1. i.e. log(n)
• Height of a complete binary tree with 'n' nodes = log with base 2 of n. i.e. log(n)

Cost of operations on a tree depends on height of a tree. i.e. search, insert, delete operations are directly proportional to the height of a tree.

The height of a tree is minimum if the tree is densly populated, i.e. tree is a perfect binary tree or close to complete binary tree. For 'n' nodes, minimum height of a tree can be log(n). So, the best time complexity with trees possible is O(log n).

For sparsely populated tree (which can be a linked list in worst case) the height becomes maximum, so cost of operations also increase. For 'n' nodes, maximum height can be (n-1). So, the worst case time complexity while dealing with trees can be o(n).

Balanced Binary Tree

Because of the above reason, we try to keep the height of a tree as minimum as possible. To do this, we try to keep the binary tree balanced.

A tree is said to be balanced binary tree if the difference between height of left and right subtree for every node is not more than 'k', which is mostly 1. This difference at any node is calculated as:

Difference = | height of left subtree - height of right subtree |